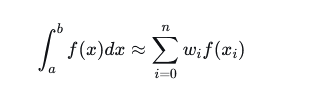Firstly, we introduce the Python language with a few simple examples.
According to programming tradition, the first program in Python should be ‘Hello, World’. As you might expect, it is written as follows:
print("hello,world!")
If the code is intended to run on Linux or Unix systems, a few lines can be added to the beginning of the source code file:
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
The first line specifies the interpreter to execute the Python script, while the second line indicates the file encoding used.
Next, the simplest calculator example using Python comes on stage:
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
x = 11 + (99 - 235) * 2.565
print(x)
Of course, more complex calculations can still be easily performed with Python.
By the way, x is a variable. You don’t have to declare a variable before using it.
Python has some functions for strings, for example:
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
# Define a string for examples
my_string = "hello, world! welcome to python."
# 1. len() - Returns the length of the string (number of characters)
length = len(my_string)
print(f"The length of the string is: {length}")
# Output: The length of the string is: 32
# 2. upper() - Converts all letters in the string to uppercase
uppercase_string = my_string.upper()
print(f"Uppercase: {uppercase_string}")
# Output: Uppercase: HELLO, WORLD! WELCOME TO PYTHON.
# 3. lower() - Converts all letters in the string to lowercase
lowercase_string = "HELLO Python".lower()
print(f"Lowercase: {lowercase_string}")
# Output: Lowercase: hello python
# 4. split() - Splits the string into a list based on specified separator
# Default separator is space
words = my_string.split()
print(f"Split by space: {words}")
# Output: Split by space: ['hello,', 'world!', 'welcome', 'to', 'python.']
# Use comma as separator
parts = my_string.split(',')
print(f"Split by comma: {parts}")
# Output: Split by comma: ['hello', ' world! welcome to python.']
# 5. strip() - Removes leading and trailing whitespace characters (or specified characters)
text_with_spaces = " some text "
cleaned_text = text_with_spaces.strip()
print(f"Stripped: '{cleaned_text}'")
# Output: Stripped: 'some text'
# 6. replace() - Replaces a substring within the string
new_string = my_string.replace("world", "Python")
print(f"After replacement: {new_string}")
# Output: After replacement: hello, Python! welcome to python.
# 7. find() - Finds the first occurrence of a substring, returns -1 if not found
position = my_string.find("world")
print(f"'world' found at position: {position}")
# Output: 'world' found at position: 7
# 8. startswith() - Checks if the string starts with the specified prefix
starts_with_hello = my_string.startswith("hello")
print(f"Starts with 'hello': {starts_with_hello}")
# Output: Starts with 'hello': True
# 9. endswith() - Checks if the string ends with the specified suffix
ends_with_python = my_string.endswith("python.")
print(f"Ends with 'python.': {ends_with_python}")
# Output: Ends with 'python.': True
# 10. capitalize() - Converts the first character to uppercase and the rest to lowercase
capitalized_string = my_string.capitalize()
print(f"Capitalized: {capitalized_string}")
# Output: Capitalized: Hello, world! welcome to python.
# 11. title() - Converts the first character of each word to uppercase
title_string = my_string.title()
print(f"Title case: {title_string}")
# Output: Title case: Hello, World! Welcome To Python.
The following Python program shows how to manipulate an array.
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
#defining a list
x=[1,2,3,4,5]
#iterating through each element in the list
for y in x :
print(y)
#modifying every element by multiplying it.
for i in range(len(x)):
x[i]=x[i]*10
print(x)
#the following code block can't change any element
for z in x:
z=z*10
print(x)
# We accumulate the current element into the sum and update the element with the sum in each iteration.
for i in range(1,len(x)):
x[i]=x[i-1]+x[i]
print(x)
#
for (x1,x2) in zip(x,list(reversed(x))):
print(x1+x2)
# the slice of array
print("-----------")
print(x)
for i in range(len(x)):
print(x[-i])
print(x[i])
print(x[i:])
print(x[:-i])
we start the explanation of the code above.
x is a variable.
Both for y in x and for i in range(len(x)): complete an iteration. The difference between them is that the first approach creates a new variable that receives the value of each element directly, while the second uses an index to reference each element; that means the first one is unable to change the elements in x and the second one can modify the elements in x.
x[-i] selects the i-th element from the end of the list. For example, if i = 1, it returns the last element.
x[:-i] returns a slice containing all elements from the start up to but excluding the i-th element from the end. For example, x[:-1] returns all elements except the last one.
the result of running the code below is as follows.
1
2
3
4
5
[10, 20, 30, 40, 50]
[10, 20, 30, 40, 50]
[10, 30, 60, 100, 150]
160
130
120
130
160
-----------
[10, 30, 60, 100, 150]
10
10
[10, 30, 60, 100, 150]
[]
150
30
[30, 60, 100, 150]
[10, 30, 60, 100]
100
60
[60, 100, 150]
[10, 30, 60]
60
100
[100, 150]
[10, 30]
30
150
[150]
[10]
Second, we will present the concept of numerical integration with some Python code.
can be used to compute the approximate value of definite integrals, particularly in cases where we cannot find an antiderivative, or the antiderivative is highly complicated.
The key idea is to convert the continuous integral into a discrete sum.
The scipy.integrate library provides powerful functions for numerical integration.
import numpy as np
from scipy import integrate
# Define the integrand
def f(x):
return np.sin(x) * np.exp(-x)
# Integration Interval
a, b = 0, np.pi
# 1. Using quad (based on adaptive Simpson and Gaussian quadrature methods)
result_quad, error_quad = integrate.quad(f, a, b)
print(f"quad result: {result_quad:.10f}, Estimated Error: {error_quad:.2e}")
# 2. Using fixed_quad (fixed-order Gaussian quadrature)
result_gauss, _ = integrate.fixed_quad(f, a, b, n=5)
print(f"5-Point Gaussian Quadrature Result: {result_gauss:.10f}")
# 3. Using the trapezoidal rule"
x_trap = np.linspace(a, b, 100) # generate 100 nodes
y_trap = f(x_trap)
result_trap = np.trapz(y_trap, x_trap)
print(f"Composite Trapezoidal Rule Result (100 points): {result_trap:.10f}")
# 4. Using Simpson's rule
result_simps = integrate.simpson(y_trap, x_trap)
print(f"Composite Simpson's Rule Result (100 points): {result_simps:.10f}")
# The exact value is provided for comparison (this example has an analytical solution)
exact = (1 + np.exp(-np.pi)) / 2
print(f"Exact Value: {exact:.10f}")
The popular methods for numerical integration are Simpson’s rule and the trapezoidal rule.
- trapezzoidal rule
The area of a rectangle can be used to approximate the area of a trapezoid.
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
import numpy as np
# Compare with Scipy's results
from scipy import integrate
def trapezoidal_rule(f, a, b, n):
"""
Compute the approximate value of definite integral using composite trapezoidal rule
Parameters:
f: integrand function
a: lower limit of integration
b: upper limit of integration
n: number of subintervals
Returns:
integral: approximate value of the integral
"""
# Calculate step size
h = (b - a) / n
# Calculate x values of all nodes
x = np.linspace(a, b, n + 1)
# Calculate function values at all nodes
y = f(x)
# Apply trapezoidal rule formula
# First term f(a) and last term f(b) have coefficient 1,
# middle terms have coefficient 2
integral = (h / 2) * (y[0] + 2 * np.sum(y[1:n]) + y[n])
return integral
# Test function
def f(x):
return np.sin(x) + np.cos(x)
# Integration parameters
a, b = 0, np.pi # Integration interval
n = 100 # Number of subintervals
# Using self-implemented function
my_result = trapezoidal_rule(f, a, b, n)
# Using Scipy's trapezoidal rule
x_scipy = np.linspace(a, b, n + 1)
y_scipy = f(x_scipy)
scipy_result = np.trapz(y_scipy, x_scipy)
# Using Scipy's quad function to obtain high-precision result
quad_result, error = integrate.quad(f, a, b)
print("Method comparison:")
print(f"Custom trapezoidal rule: {my_result:.10f}")
print(f"NumPy trapezoidal rule: {scipy_result:.10f}")
print(f"Scipy quad (high precision): {quad_result:.10f}")
print(f"Difference between two trapezoidal methods: {abs(my_result - scipy_result):.2e}")
2.Simpson’s rule
It uses parabolas to approximate the curve f(x), achieving higher accuracy.
import numpy as np
from scipy import integrate
def simpsons_rule(f, a, b, n):
"""Composite Simpson's rule implementation"""
if n % 2 != 0:
n += 1
h = (b - a) / n
x = np.linspace(a, b, n + 1)
y = f(x)
coefficients = np.ones(n + 1)
coefficients[1:n:2] = 4
coefficients[2:n-1:2] = 2
return (h / 3) * np.dot(coefficients, y)
# Test function
def f(x):
return np.sin(x) + np.cos(x)
# Integration parameters
a, b = 0, np.pi
n = 100 # Number of subintervals
# Compare various methods
my_result = simpsons_rule(f, a, b, n)
# Scipy's Simpson's rule
x_scipy = np.linspace(a, b, n + 1)
y_scipy = f(x_scipy)
scipy_result = integrate.simpson(y_scipy, x_scipy)
# Scipy high-precision integration
quad_result, error = integrate.quad(f, a, b)
# Trapezoidal rule comparison
trapz_result = np.trapz(y_scipy, x_scipy)
print("Method comparison:")
print(f"Custom Simpson's rule: {my_result:.10f}")
print(f"Scipy Simpson's rule: {scipy_result:.10f}")
print(f"Scipy quad (high precision): {quad_result:.10f}")
print(f"NumPy trapezoidal rule: {trapz_result:.10f}")
print()
print(f"Error of Simpson's rule vs exact value: {abs(my_result - quad_result):.2e}")
print(f"Error of trapezoidal rule vs exact value: {abs(trapz_result - quad_result):.2e}")