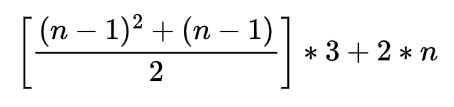Quantas cartas tem em uma torre de cartas com N andares?

Por que esta pergunta?

Você pode estar se perguntando: por que devo saber responder uma pergunta como essa? Isso faz alguma diferença na minha vida?

Pois bem, eu nunca entendi a força de uma pergunta (e resposta) como essa, até uma recente experiência, então decidi compartilhá-la com a comunidade, para dar exemplo de como os detalhes podem fazer imensa diferença.

Recentemente participei de um happy hour promovido pela empresa que eu trabalho atualmente (woovi).

Todos nós chamamos um motorista de aplicativo, e o CTO veio conosco no carro.

Durante o fluir da conversa, chegamos ao assunto matemática.

Eu gosto de matemática, sempre me dei bem desde o colégio.

O CTO queria nos mostrar como, às vezes, perguntas simples podem nos levar a raciocínios complexos e como a matemática é o melhor método para ordenar a razão humana.

Então ele fez a seguinte pergunta:

Quantas cartas tem em uma torre de cartas com 10 andares?

Confesso que isso me chamou a atenção logo de cara, é o tipo de pergunta que ajuda a dar um maior sentido para a minha vida, então decidi tentar até conseguir.

Estávamos todos no carro, a caminho do happy hour.

O meu celular estava sem internet, então não tinha como usar nenhuma ajuda externa; era eu e o problema.

Fiquei uns 20 minutos pensando, consegui chegar a uma fórmula que parecia resolver a questão, fiz as contas de cabeça e respondi:

152.

Na conferência, viram que estava errado; o correto era 155. Errei por 3 cartas.

Vi que tinha cometido alguns erros de raciocínio e de cálculo.

Pensei mais profundamente sobre o problema, corrigi a minha fórmula e o meu cálculo, com isso cheguei à resposta 155.

Não disse o valor de imediato, visto que sei que a grande capacidade da mente humana é saber lidar com raciocínio abstrato, então decidi proclamar primeiro a fórmula para depois o resultado.

Todos acharam legal o ocorrido, estamos perto do destino, mas conseguiram validar que a fórmula produzia valores corretos.

Este assunto chegou até o nosso happy hour, gostaram de saber, mas fizeram a pergunta que faz qualquer um tremer: por que esta fórmula é correta? Como chega-se nela?

Como cheguei à resposta?

Eu não conseguia explicar de uma forma fácil como tinha chegado na resposta, isso gerou confusão em alguns.

Então decidi corrigir essa questão, simplifiquei a fórmula e o raciocínio para chegar até lá, está a fórmula simplificada:

O meu raciocínio se deu da seguinte forma:

• Separe a torre em células de três cartas como essa.

Resolvendo com 1 andar:

• Observe que, em uma torre com 1 andar, só cabe uma célula.
• Logo, poderíamos deduzir que, em uma torre com um andar, serão necessárias 3 cartas, mas isso apenas se quisermos montar a torre com as cartas da base também. Como queremos a torre sem a base, temos que descontar a base.
• Logo, a dedução correta seria: uma célula vezes 3 cartas menos a base, 1*3 – 1 = 2.

Resolvendo com 2 andares:

• Vamos seguir a mesma linha de raciocínio anterior, mas com um degrau a mais, e ver o que mudou.
• Para fins didáticos, conte os andares de cima para baixo.
• Observe que no 1° andar ainda temos 1 célula; no 2° andar, 2 células.
• Observe também que temos 2 cartas de base no segundo andar.
• Com isso, podemos deduzir que a conta seria a seguinte: uma célula do 1° andar, mais 2 células do 2° andar, menos as 2 cartas da base, (1+ 2) * 3 – 2 = 7.

Entendendo o padrão

Apesar de ser poucos exemplos, conseguimos observar alguns padrões aqui:

• A quantidade de células por andar é igual ao número do andar, logo deduz: 1° andar -> 1 célula, 2° andar -> 2 células, etc…
• A quantidade de cartas na base também é igual ao número do andar, então entendemos que: 1° andar -> 1 carta na base, 2° andar -> 2 cartas na base.

Com essas observações, já conseguimos deduzir que, para chegar ao total de cartas contidas em uma torre de cartas com N andares, devemos:

1. Somar o total de células contidas em cada andar.
2. Multiplicar o total de células pela quantidade de cartas em cada célula (nesse caso, 3).
3. Pegar o resultado e subtrair as cartas que estão na base da torre (sempre será igual à quantidade de andares na torre).

Montando a fórmula

O raciocínio é bem simples, na verdade, mas você pode ter se deparado com um problema logo de cara.

como somar todas as células presente em todos os andares?
se tiver 100 andares, vou ter que somar 100 + 99 + 98 … + 2 + 1?

A sua dúvida é bem pertinente, na verdade, mas tem uma solução fácil.

A grande maioria das pessoas conhece o operador matemático fatorial (símbolo: !), mas, fora ele, existem diversos outros, entre eles o operador termial (símbolo: ?), que atende exatamente essa demanda.

Ao estudarmos o operador terminal, descobrimos que podemos usar a seguinte fórmula para resolver a questão mais facilmente e nos poupar esse trabalho massante:

Se usarmos essa fórmula como a solução base para o primeiro passo da solução, basta adicionar as operações do segundo e terceiro passo e teremos a fórmula completa (não simplificada):

Simplificando um pouco mais a fórmula

Nós conseguimos reduzir um pouco a complexidade ao simplificarmos uma operação da nossa fórmula.

Observe que temos 2 constantes na nossa fórmula:

A divisão por dois da fração e a multiplicação por três podemos unir as duas em uma única operação de multiplicação, visto que:

Com isso, podemos simplificar a fórmula para:

Agradecimentos

Muito obrigado a você, leitor, que veio até aqui.

Acompanhar uma linha de raciocínio como essa não é um privilégio de todos.

Também quero agradecer ao meu CTO que me incentivou a escrever esse artigo.