Welcome to Day 2 of the Statistics Challenge for Data Scientists.
In today’s post, we’ll break down some of the most important — and often misunderstood — statistical concepts used in data science.
You’ll learn about correlation, causation, outliers, and other key terms every data scientist must understand before analyzing data or building models.
Why These Concepts Matter
Statistics is the foundation of data science.
Every time you explore data, detect patterns, or evaluate a model, you’re applying statistical thinking — often without realizing it.
Understanding these concepts helps you avoid misleading conclusions and improves your ability to interpret results accurately.
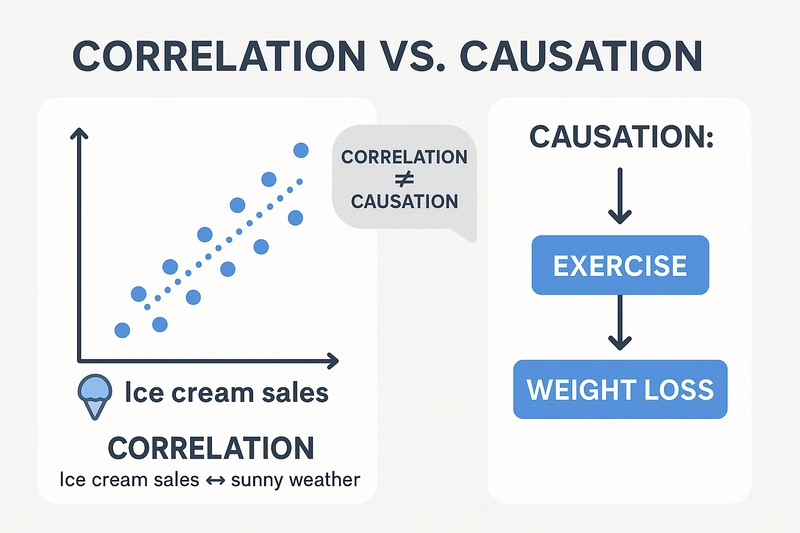
1. Correlation — How Variables Move Together
Definition:
Correlation measures how two variables move in relation to each other.
If one variable changes, correlation tells you whether the other tends to change in the same or opposite direction, and how strongly.
| Type | Meaning | Example |
|---|---|---|
| Positive Correlation | Both variables increase or decrease together. | As temperature rises, ice cream sales increase. |
| Negative Correlation | One increases while the other decreases. | As car speed increases, travel time decreases. |
| Zero Correlation | No consistent relationship between them. | Shoe size and IQ score. |
Mathematically:
The Pearson correlation coefficient (r) ranges from –1 to +1.
- +1: Perfect positive correlation
- –1: Perfect negative correlation
- 0: No correlation
Example:
If r = 0.85, there’s a strong positive relationship.
If r = -0.75, there’s a strong negative relationship.
Important Note:
Correlation only measures association — it does not imply causation.
2. Causation — When One Variable Truly Affects Another
Definition:
Causation means that a change in one variable directly causes a change in another.
Example:
- Increasing the temperature causes water to boil faster.
- Smoking causes lung diseases.
So, while correlation tells you “these two things move together,” causation tells you “this thing happens because of that.”
3. Correlation vs. Causation — The Common Confusion
| Concept | What It Means | Example |
|---|---|---|
| Correlation | Two variables change together, but one doesn’t necessarily cause the other. | Number of firefighters and fire damage — both rise together, but fires cause both. |
| Causation | One variable directly influences the other. | Increasing study hours causes better exam results. |
Remember:
Just because two things are correlated doesn’t mean one causes the other.
Often, a third hidden variable (confounder) is influencing both.
Example:
Ice cream sales and drowning cases are positively correlated — but ice cream doesn’t cause drowning.
The hidden variable is temperature (people swim and eat ice cream more in summer).
4. Outliers — The Unusual Data Points
Definition:
An outlier is a data point that differs significantly from other observations.
It’s an extreme value that doesn’t fit the general trend.
Example:
If most people in a dataset are aged 20–50, and one person is 95, that’s an outlier.
How to Detect Outliers:
Why They Matter:
Outliers can distort:
- The mean (average)
- Model performance
- Visual interpretations
Handling Outliers:
- Investigate the cause first (error or valid observation?)
- Apply transformation or remove if they mislead analysis
- Use robust models (e.g., median-based or tree-based models) that are less affected by outliers.
5. Key Statistical Terminologies Every Data Scientist Should Know
| Term | Simple Explanation | Example |
|---|---|---|
| Population | The entire group you want to study. | All customers of a bank. |
| Sample | A subset of the population used for analysis. | 1,000 randomly chosen customers. |
| Variable | A measurable characteristic. | Age, salary, gender. |
| Feature | A variable used in modeling. | Income level or transaction amount. |
| Mean (Average) | Sum of all values ÷ number of values. | Average monthly income. |
| Median | Middle value when data is sorted. | Useful when data has outliers. |
| Mode | Most frequently occurring value. | Most common product category purchased. |
| Variance | How far data points spread from the mean. | High variance → data widely spread. |
| Standard Deviation (SD) | Square root of variance; measures data spread in the same units as data. | Low SD → data close to mean. |
| Normal Distribution | Bell-shaped curve; most data near mean. | Heights, test scores. |
| Skewness | Asymmetry in data distribution. | Right-skewed: income data. |
| Kurtosis | Measures how heavy or light the tails of a distribution are. | High kurtosis → more outliers. |
| P-Value | Probability that observed results happened by chance. | Low p (<0.05) → statistically significant. |
| Confidence Interval | Range of values likely to contain the true population parameter. | 95% CI means we’re 95% confident the true value lies in this range. |
| Hypothesis Testing | Procedure to test assumptions about data. | Testing if marketing campaign improved sales. |
6. Visualizing Relationships: Correlation Heatmap
A correlation heatmap helps visualize relationships among variables in a dataset.
Example:
- High positive correlation → bright color (e.g., red)
- High negative correlation → dark color (e.g., blue)
- Near zero correlation → neutral color (white)
Such visuals help data scientists identify which features might be useful or redundant for modeling.
7. Summary — Building Statistical Intuition
| Concept | Key Idea | Why It Matters |
|---|---|---|
| Correlation | Two variables move together | Shows association |
| Causation | One variable directly affects another | Shows cause-effect relationship |
| Outliers | Unusual extreme values | Can distort results |
| Variance & SD | Measure data spread | Help understand data distribution |
| Mean/Median/Mode | Central tendency measures | Summarize data behavior |
Pro Tip
Before applying machine learning, always understand your data statistically first.
Clean, explore, visualize, and question relationships — this is what separates a good data scientist from a great one.
What’s Next
On Day 3, we’ll explore Probability and Distributions — understanding how randomness and uncertainty are modeled in data science.
Follow the #StatisticsChallenge to strengthen your foundation, one concept at a time.